Solving Large Systems of Linear Simultaneous Equations

NICOLE LESIRIMA

METHODS OF SOLVING LARGE SYSTEMS OF LINEAR SIMULTANEOUS EQUATIONS

What Citation Formats Do You Support?

We hear “Can you write in APA or MLA?” all the time—and the answer’s a big yes, plus way more! Our writers are wizards with every style—APA, MLA, Harvard, Chicago, Turabian, you name it—delivering flawless formatting tailored to your assignment. Whether it’s a tricky in-text citation or a perfectly styled reference list, they’ve got the skills to make your paper academically spot-on.

1. PROJECT DESCRIPTION

Linear systems simulate real-world problems using applied numerical procedure. The main aim of this project is to consider what factors affect the efficiency of the various methods of solving linear simultaneous equations. So far, one of the main factors is rounding errors that can produce inaccurate solutions. Moreover, MATLAB programs have been produced to time the calculation speed to determine the efficiency of the methods. Generally, these methods are subdivided into two; direct and iterative methods. Direct methods are commonly used to solve small systems of equations. The iterative methods are used to solve real-world problems that produce systems of equations for which the coefficient matrices are sparse.

The relevance of studying these methods have its real world applications. The real world applications can be seen in various fields such as science and engineering, accounting and finance, business management and in operational research. The approach provides a logical framework for solving complex decisions in a wide range of industries. The advantage is that, decisions are founded on data analysis.

Environmentalists and meteorologists may use large systems of simultaneous linear equations to predict future outcomes. For instance, to predict weather patterns or climate change, a large volume of data is collected over a long span of time on many variables including, solar radiation, carbon emissions and ocean temperatures. Queen Mary University of London (2015). This data is represented in the form of a transition matrix that has to be row reduced into a probability matrix that can then be used in the prediction of climate change.

The objective of an enterprise is to maximize returns while maintaining minimum costs. Whereas the use of large systems of simultaneous linear equations may provide a basis for evidence based business decision making in an enterprise, it is important to know which linear systems are most appropriate in order to minimize undesirable outcomes for an enterprise.

Are Paper Services Legal?

Yes, completely! They’re a valid tool for getting sample papers to boost your own writing skills, and there’s nothing shady about that. Use them right—like a study guide or a model to learn from—and they’re a smart, ethical way to level up your grades without breaking any rules.

2. PROJECT REPORT OUTLINE

Chapter 1

Introduction

Large systems of linear simultaneous equations are used to simulate real-world problems using applied numerical procedure. The real world applications can be seen in various fields such as science and engineering, accounting and finance, business management. The approach provides a logical framework for solving complex decisions in a wide range of industries. The advantage is that decisions are founded on data analysis. The aim of this project is to explore the efficiency of a large systems of linear simultaneous equations in the optimal decision making of an enterprise.

How Much for a Paper?

Prices start at $10 per page for undergrad work and go up to $21 for advanced levels, depending on urgency and any extras you toss in. Deadlines range from a lightning-fast 3 hours to a chill 14 days—plenty of wiggle room there! Plus, if you’re ordering big, you’ll snag 5-10% off, making it easier on your wallet while still getting top-notch quality.

Chapter 2

Direct Methods: Gaussian Elimination and LU Factorisation

Direct methods of solving linear simultaneous equations are introduced. This chapter will look at the Gaussian Elimination and LU Factorisation methods. Gaussian Elimination involves representing the simultaneous equations in an augmented form, performing elementary row operations to reduce the upper triangular form and finally back substituting to form the solution vector. LU Factorisation on the other hand is where a matrix A finds a lower triangular matrix L and an upper triangular matrix U such that A = LU. The purpose of this lower triangular matrix and upper triangular matrix is so that the forward and backward substitutions can be directly applied to these matrices to obtain a solution to the linear system. An operation count and computing times using MATLAB is calculated so as to determine the best method to use.

Chapter 3

Will Anyone Find Out I Used You?

Nope—your secret’s locked down tight. We encrypt all your data with top-tier security, and every paper’s crafted fresh just for you, run through originality checks to prove it’s one-of-a-kind. No one—professors, classmates, or anyone—will ever know you teamed up with us, guaranteed.

Cholesky Factorisation

Introduction to the Cholesky method. This is a procedure whereby the matrix A is factorised into the product of a lower triangular matrix and its transpose; the forward and backward substitutions can be directly applied to these matrices to obtain a solution. A MATLAB program is written to compute timings. A conclusion can be drawn by comparing the three methods and determining which is the most suitable method that will produce the most accurate result as well as take the shortest computing time.

Chapter 4

Iterative Methods: Jacobi Method and Gauss-Seidel

Do You Rely on AI?

Not even a little—our writers are real-deal experts with degrees, crafting every paper by hand with care and know-how. No AI shortcuts here; it’s all human skill, backed by thorough research and double-checked for uniqueness. You’re getting authentic work that stands out for all the right reasons.

This chapter will introduce the iterative methods that are used to solve linear systems with coefficient matrices that are large and sparse. Both methods involve splitting the matrix A into lower triangular, diagonal and upper triangular matrices L, D, U respectively. The main difference comes down to the way the x values are calculated. The Jacobi method uses the previous x values (n) to calculate the next iterated x values (n+1). The Gauss-Seidel uses the new x value (n+1) to calculate the x₂ value.

Chapter 5

Successive Over Relaxation and Conjugate Gradient

Other iterative methods are introduced. The Successive Over Relaxation method over relaxes the solution at each iteration. This method is calculated using the weighted sum of the values from the previous iteration and the values form the Gauss-Seidel method at the current iteration. The Conjugate Gradient method involves improving the approximated value of x_k to the exact solution which may be reached after a finite number of iterations usually smaller than the size of the matrix.

Why Are You Top for Research Papers?

Our writers are Ph.D.-level pros who live for nailing the details—think deep research and razor-sharp arguments. We pair that with top plagiarism tools, free revisions to tweak anything you need, and fast turnarounds that don’t skimp on quality. Your research paper won’t just shine—it’ll set the bar.

Chapter 6

Conclusion

All the project findings and results are summarised in this chapter. Conclusion can be made from both direct methods and iterative methods whereby the most accurate method with the shortest computing time can be found. Drawbacks from each method will be mentioned as well its suitability for solving real world problems.

3. PROGRESS TO DATE

The project to date has covered the direct methods of solving simultaneous equations.

Who’s Behind My Essays?

You’re in good hands with degree-holding pros—many rocking Master’s or higher—who’ve crushed our tough vetting tests in writing and their fields. They’re your partners in this, hitting tight deadlines and academic standards with ease, all while tailoring every essay to your exact needs. No matter the topic, they’ve got the chops to make it stellar.

Gaussian Elimination

This involves representing the simultaneous equations in an augmented form, performing elementary row operations to reduce the upper triangular form and finally back substituting to form the solution vector. For example, to solve an mxn matrix:

Ax = b

The aim of the Gaussian elimination is to manipulate the augmented matrix [A|b] using elementary row operations; by adding a multiple of the pivot rows to the rows beneath the pivot row i.e. R_i‬‬‬‬ R_i +kR_j. Once the augmented matrix is in the row echelon form, the solution is found using back substitution.

Is My Paper Original?

100%—we promise! Every paper’s written fresh from scratch—no AI, no copying—just solid research and proper citations from our expert writers. You can even request a plagiarism report to see it’s 95%+ unique, giving you total confidence it’s submission-ready and one-of-a-kind.

The following general matrix equation has been reduced to row echelon form:

This corresponds to the linear system

Rearranging the final solution is given by

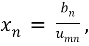
For all other equations

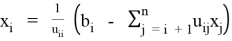i = n – 1, . . .,

How Do I Get Started?

It’s super easy—order online with a few clicks, then track progress with drafts as your writer works their magic. Once it’s done, download it from your account, give it a once-over, and release payment only when you’re thrilled with the result. It’s fast, affordable, and built with students like you in mind!

The operation count and timing the Gaussian Elimination was performed. The total number of operations for an nxn matrix using the Gaussian elimination is with O(N³).

LU Factorisation

How Fast for Rush Jobs?

We can crank out a killer paper in 24 hours—quality locked in, no shortcuts. Just set your deadline when you order, and our pros will hustle to deliver, even if you’re racing the clock. Perfect for those last-minute crunches without compromising on the good stuff.

This is where a matrix A finds a lower triangular matrix L and an upper triangular matrix U such that A = LU. The purpose of this lower triangular matrix and upper triangular matrix is so that the forward and backward substitutions can be directly applied to these matrices to obtain a solution to the linear system.

In general,

L and U is an m x n matrix:

L =  U = 

For higher order matrices, we can derive the calculation of the L and U matrices. Given a set of n elementary matrices E₁, E₂,…, Enapplied to matrix A, row reduce in row echelon form without permuting rows such that A can be written as the product of two matrices L and U that is

Can You Handle Complex Subjects?

For sure! Our writers with advanced degrees dive into any topic—think quantum physics or medieval lit—with deep research and clear, sharp writing. They’ll tailor it to your academic level, ensuring it’s thorough yet easy to follow, no matter how tricky the subject gets.

A = LU,

Where

U = E_n…E₂E₁A,

L = E₁^-1 E₂^-1…E_n^-1 

For a general nxn matrix, the total number of operations is O(N³). A Matlab program has been produced to time the LU Factorisation. So far, this method has proven more efficient than the Gaussian Elimination.

How Do You Meet Prof Standards?

We stick to your rubric like glue—nailing the structure, depth, and tone your professor wants—then polish it with edits for that extra shine. Our writers know what profs look for, and we double-check every detail to make sure it’s submission-ready and grade-worthy.

Cholesky Factorisation

This is a procedure whereby the matrix A is factorised into the product of a lower triangular matrix and its transpose i.e. A = LL^T  or

  =   

The Cholesky factorisation is only possible if A is a positive definite. Forward and backward substitution is employed in finding the solutions.

The method was also timed at it can be concluded that it is the most effective and efficient direct method for solving simultaneous equations.

The indirect methods have been introduced with a short outline of what each method entails.

4. Work Still to be Completed    

As from the objectives layed out from the terms of reference, the following are the objectives that are yet to be completed.

1. Week 13 – 16: Evaluating the convergence rate of the iterative methods in detail as well as finding out which method improves the solution efficiency.  Production of MATLAB programs analysing the different methods and other methods. Over the next 3 weeks, the conditions for convergence will be analysed. One of the most important conditions that will be studied is the spectral radius. This is a condition applied on the indirect methods to determine how fast or slow a method takes to achieve the state of convergence. Moreover, the project will also produce Matlab programs for the iterative methods and employ the spectral radius on these programs to determine the speed of convergence for large sparse matrices.

2. Weeks 17 – 19: Introduction to the Successive Over-Relaxation (SOR) method and the Conjugate Gradient method. Successive Over-Relaxation method improves the rate of convergence of the Gauss-Siedel method by over-relaxing the solution at every iteration. While the Conjugate Gradient improves the approximated value of x to the exact solution. Matlab programs will be produced for the two methods together with the speed of convergence of different sizes of matrices.

3. Week 20 – 24:Writing the findings and conclusions of the report, finalising on the bibliography and doing a review of the project as a whole.  Preparing oral and poster presentation.