Beer-Lambert’s Law Experiment

Design Project on Beer- Lambert’s Law.

• Saswati Rakshit

Aim:

What Citation Styles Can You Use for My Essay?

Students often ask, “Can you write my essay in APA or MLA?”—and the answer’s a big yes! Our writers are experts in every style imaginable: APA, MLA, Chicago, Harvard, you name it. Just tell us what you need, and we’ll deliver a perfectly formatted paper that matches your requirements, hassle-free.

To learn and understand the basics and mathematical calculations of the following problem and write programs accordingly.

Problem 1: Suppose an outdoor multispectral image is captured by a camera with a path length of 1-3 microns. A part of the intensity is attenuated by the absorption of small particles in the atmosphere for that spectral range and let the scattering by the small particles for that spectral range is 0.

Find the total attenuation in the spectral range using Simpson 1/3 ­, trapezoidal and Euler integration methods and comment in your findings.

Scope/Application:

Is It Legal to Use Your Writing Service?

Absolutely, it’s 100% legal! Our service provides sample essays and papers to guide your own work—think of it as a study tool. Used responsibly, it’s a legit way to improve your skills, understand tough topics, and boost your grades, all while staying within academic rules.

Beer Lambert’s law relates the attenuation of light to the properties of the material through which the light is passing. When light passes through a medium some amount of light is absorbed by the medium. For this absorption intensity of light reduces.

Beer Lambert’s law states that the quantity of light absorbed is directly proportional to the concentration of the substance and the path length of the light through the transmission medium

Beer Lambert’s law is used to find total attenuation of light when light passes through a medium(considering scattering is zero).It is also used to find the concentration of medium in chemical analysis, medium length in some application and absorbance of medium when necessary.

How Much Does It Cost to Get a Paper Written?

Our pricing starts at $10 per page for undergrad work, $16 for bachelor-level, and $21 for advanced stuff. Urgency and extras like top writers or plagiarism reports tweak the cost—deadlines range from 14 days to 3 hours. Order early for the best rates, and enjoy discounts on big orders: 5% off over $500, 10% over $1,000!

Introduction of Beer Lambert Law:

Lambert’s law is (Related to thickness/path length of medium)

When light passes through an absorbing medium its intensity decreases exponentially as the path length of the absorbing medium increases.

I = I₀ e^{-k1 L ……………………………………….(i)}

Will My Use of This Service Stay Private?

Yes, totally! We lock down your info with top-notch encryption—your school, friends, no one will know. Every paper’s custom-made to blend with your style, and we check it for originality, so it’s all yours, all discreet.

(where L is the length of medium and k1 is molar extinction/absorption co-efficient for the absorbing material)

Beer’s law is (Related to concentration of absorbing medium)

When light passes through medium(absorbing) its intensity decreases exponentially as the concentration of the absorbing medium increases.

I = I₀e^{-k2C …………………………………..(ii)}

Do You Use AI to Write Papers?

No way—our papers are 100% human-crafted. Our writers are real pros with degrees, bringing creativity and expertise AI can’t match. Every piece is original, checked for plagiarism, and tailored to your needs by a skilled human, not a machine.

(C concentration of medium and k2 is absorption co-efficient for the absorbing material)

Combining both Beer’s and Lambert’s law we get

I = I₀ e-^k3CL combining eqn (i) and (ii)

Where I₀ = Incident light intensity

Why Choose You for Research Papers?

We’re the best because our writers are degree-holding experts—Bachelor’s to Ph.D.—who nail any topic. We obsess over quality, using tools to ensure perfection, and offer free revisions to guarantee you’re thrilled with the result, even on tight deadlines.

I = Transmitted Light intensity

C=concentration / volume

L= path length of medium

We consider an outdoor multispectral image is captured by a camera with a spectral range of 1-3 microns. A part of the intensity is attenuated by the absorption of small particles in the medium.so image will be attenuated. Beer Lambert’s law find the attenuation caused by absorption for that spectral range and let the scattering by the small particles for that spectral range is 0.

Who’s Writing My College Essays?

Our writers are top-tier—university grads, many with Master’s degrees, who’ve passed tough tests to join us. They’re ready for any essay, working with you to hit your deadlines and grading standards with ease and professionalism.

Objectives:

In a given path length 1 to 3 micron, we have considered a constant value of molar extinction/absorption co-efficient.and now we need to find the absorbance & total attenuation of the incident light using Beer’s Lambert Law. And then applying Simpson’s 1/3, Trapezoidal and Euler Integration in it compare the result.

System flow:

Implementation of the Beer Lambert’s law needs a proper mathematical understanding of the Beer Lambert’s law. Here I am showing how to set the equation using its mathematical basics

Are Your Papers Original?

Always! We start from scratch—no copying, no AI—just pure, human-written work with solid research and citations. You can even get a plagiarism report to confirm it’s 95%+ unique, ready for worry-free submission.

First we apply Beer Lambert’s Law for a medium which absorbs light in spectral range 1-3 micron. Considering no scattering we assume I₀ is the incident light to the medium Air of attenuation coefficient 1.64at temperature 20^oC. Here path length travelled by light is 1 to 3 micron.

According to Beer Lambert’s law light intensity is decreased if concentration & path length increase.

So we get the equation I=I_o e^-kcl = I_o e^-µl

Now as we know the path length l and attenuation coefficient µ, we calculate absorbance of the medium using eqn

Can You Match Any Citation Style?

You bet! From APA to IEEE, our writers nail every style with precision. Give us your guidelines, and we’ll craft a paper that fits your academic standards perfectly, no sweat.

Log₁₀ = kcl (Where l is constant)

= e ^kcl

But now for a spectral range 1 to 3 micron path length we need to formulate a new equation by integrating ranged from .001mm to .003 mm

[Here x is path length and c is attenuation coefficient]

Can I Update Instructions Mid-Order?

Yep! Use our chat feature to tweak instructions or add details anytime—even after your writer’s started. They’ll adjust on the fly to keep your essay on point.

Solving the above eqn we get total absorbance. Thus Beer Lambert’s law is successfully implemented in our problem.

Now we apply Simpson 1/3 rd, trapezoidal rule on Beer’s Lambert Law to find total attenuation.

Finally compare the result of Simpson’s 1/3 rd and Trapezoidal rule with the actual integration.

Flow Diagram:

How Do I Get an Essay Written?

Easy—place your order online, and your writer dives in. Check drafts or updates as you go, then download the final paper from your account. Pay only when you’re happy—simple and affordable!

Math:

Beer-Lambert Law Concept

Can You Tackle Complex Essay Topics?

Definitely! From astrophysics to literary theory, our advanced-degree writers thrive on tough topics. They’ll research deeply and deliver a clear, sharp paper that meets your level—high school to Ph.D.

Consider a light incident on a medium with area A and thickness dx and concentration of molecules C. Number of molecules illuminated by light of incident intensity I_x is CAdx.

Total effective area σCAdx. Probability of light being absorbed in thickness dx is

₌ dx [where dIx is the change in intensity across dx and σ is scattering coefficient]

So we can write,

= dx ………… (i)

How Do You Meet My Professor’s Standards?

We tailor your paper to your rubric—structure, tone, everything. Our writers decode academic expectations, and editors polish it to perfection, ensuring it’s grade-ready.

Now we integrate both sides of (i)

ln (I) – ln(I₀) = ln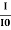 = – σCx

I = I₀e^-σCx = I₀ e^{–µx ……………….(ii)}

What’s Your Editing Process?

Upload your draft, tell us your goals, and our editors will refine it—boosting arguments, fixing errors, and keeping your voice. You’ll get a polished paper that’s ready to shine.

The co-efficient µ=σ C is the linear attenuation co-efficient. Here C=Absorbing co-efficient & σ = Scattering co-efficient.

The ibrightness of light decreases exponentially with depth in the medium.

So we can tell Beer-Lambert Law is also a function of( λ), i.e.

I (λ) = I₀ (λ) e^{-µ(λ)x………………………(iii)}

Calculation:

Can You Suggest Paper Topics?

Sure! Need ideas? We’ll pitch topics based on your subject and interests—catchy and doable. Pick one, and we’ll run with it, or tweak it together.

(Here we considered linear attenuation)

Given spectral range 0.001 mm to 0.003 mm

Let we consider Absorbing coefficient(C) of Transmission Medium (Air) = 1.64 at 20^o C. So total absorption (A) of light is calculated by integrating in the spectral range,

[from eqn ii]

= ———– (1)

=

^{= 0.002006571}

Do You Offer Rush Revisions?

Yes! If you need quick edits, our team can turn it around fast—hours, not days—tightening up your paper for last-minute perfection.

Now we can easily calculate attenuated intensity of light (I).

Attenuation is the loss of light intensity over distance. The greater the distance, the lower is the intensity

Where I=I₀ -Attenuation

Trapezoidal rule:-

We know, in case of multiple application of Trapezoidal rule, the formula is:

= [f(x₀) + 2) + f(x_n)]

Can You Provide Outlines First?

Absolutely! We’ll draft an outline based on your topic so you can approve the plan before we write—keeps everything aligned from the start.

So, here applying the above formula for equation (1) we get:

= 0.0005[[ _0.001 + 2 + [] _0.003]

= 0.0005[1.001641346 + 2.00657077 + 1.004932123]

= 0.0005[4.013144239]

=0.002006572 (Ans.)

Here,

x₀ = x_0.001, x_n = x_0.003, b = 0.003, a = 0.001, n = 2, = 0.0005.

Simpson’s rule:

Can You Include Data Analysis?

You bet! Need stats or charts? Our writers can crunch numbers and craft visuals, making your paper both sharp and professional.

We know, composite Simpson’s rule formula is written as:

= [f(x₀) + 4) +2) + f(x_n)]

So, here applying the above formula for equation (1) we get:

= 0.0003[[ _0.001 + 4 + [] _0.003]

= 0.0003[1.001641346 + 4.01314154 + 1.004932123]

= 0.001805914 (Ans.)

Here, = 0.0003.

Euler’s formula:

Here, =

y(0.001) = = 0 (assumption)

How Do You Handle Long-Term Projects?

We break it down—delivering each part on time with consistent quality. From proposals to final drafts, we’re with you all the way.

y(0.003) = ≈

and we have to find the value of equation (1) using Euler’s formula which is,

= + f (_, ) h

let us choose h = 0.001

Step-1

Can You Write for Global Standards?

Yep! Whether it’s UK, US, or Australian rules, we adapt your paper to fit your institution’s style and expectations perfectly.

i=0, = 0.001, = 0, h = 0.001

= + f (_, ) h

= 0 + f (0.001, 0) 0.001

= 0.001001641

Step-2

Is there a possibility of plagiarism in my completed order?

We write every paper from scratch just for you, and we get how important it is for you to feel confident about its originality. That’s why we double-check every piece with our own in-house plagiarism software before sending it your way. This tool doesn’t just catch copy-pasted bits—it even spots paraphrased sections. Unlike well-known systems like Turnitin (used by most universities), we don’t store or report anything to public databases, so your check stays private and safe. We stand by our plagiarism-free guarantee to ensure your paper is totally unique. That said, while we can promise no plagiarism from open web sources or specific databases we check, no tech out there (except Turnitin itself) can scan every source Turnitin indexes. If you want that extra peace of mind, we recommend running your paper through WriteCheck (a Turnitin service) and sharing the report with us.

i=1, = 0.002, = 0.001001641, h = 0.001

= + f (_, ) h

= 0.001001641 + f (0.001, 0.001001641) 0.001

= 0.0020049426

When will my order be assigned to the writer?

The moment you place your order, we jump into action to find the perfect writer for you. Usually, we’ve got someone lined up within an hour. Sometimes, though, it might take a few hours—or in rare cases, a few days—if we need someone super specialized. If no writers from your chosen category are free, we’ll suggest one from a lower category and refund the difference if you’d paid extra for that option. Want to keep tabs on things? You can always peek at your order’s status on your personal order page.

This is actually the value of the function at i.e. at (+h) or (0.002+0.001) or 0.003.

So,

=

= 0.0020049426-0

= 0.0020049426 (Ans.)

We find that the result of all above technique is almost same if we take approximation i.e.0.002.

CODES and OUTPUT:

Beer Lambert’s Law:

#include

#include

#include

int main()

{float absorbtion,m,l,u;

printf(“nEnter spectral range”);

scanf(“%f%f”,&l,&u);

printf(“nnenter the value of absorption cofficient”);

scanf(“%f”,&m);

absorbtion=(1/m)*(pow(2.718,(m*u))-pow(2.718,(m*l)));

printf(“nnTotal absorption is %f: “,absorbtion);

getch();

}

Output:

Simpson 1/3^rd rule:

#include

#include

#include

void main()

{float x[10],y[10],Total=0,h,t;

int i,n,j,k=0;

printf(“nhow many values you will enter: “);

scanf(“%d”,&n);

for(i=0; i

{ printf(“nn x%d: “,i);

scanf(“%f”,&x[i]);

printf(“nn f(x%d): “,i);

scanf(“%f”,&y[i]); }

h=x[1]-x[0];

n=n-1;

Total = Total + y[0];

for(i=1;i

{ if(k==0) { Total = Total + 4 * y[i];

k=1 }

else { Total = Total + 2 * y[i];

k=0; } }

Total = Total + y[i];

Total = Total * (h/3);

printf(“nn I = %f “, Total);

getch();}

Trapezoidal rule:

#include

#include

#include

int main(){

float x[10],y[10], Total =0,h;

int i,n,j,k=0;

float fact(int);

printf(“nhow many values of ranges you will be enter: “);

scanf(“%d”,&n);

for(i=0; i

{printf(“nn x%d: “,i);

scanf(“%f”,&x[i]);

printf(“nn f(x%d): “,i);

scanf(“%f”,&y[i]); }

h=x[1]-x[0];

n=n-1;

for(i=0;i

if(k==0) { Total = Total + y[i];

k=1; }else

Total = Total + 2 * y[i];}

Total = Total + y[i];

Total = Total * (h/2);

printf(“nn I = %f “, Total);

getch();}

Future Work & Scope:

This Beer Lambert’s law can be used in image processing application where atmospheric condition is poor to find the attenuation of light and image by absorption of light.

Implementing Euler Method.

References:

1. Weisstein, Eric W. “Simpson’s Rule.” From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/SimpsonsRule.html. (Accessed on 26.04.2015)
2. Basics of Trapezoidal and Simpson Rules, www.math.umd.edu/~jmr/141/Simpson.pdf.
3. Lal, A. K., Simpson’s Rule, 2007, http://numericalmethods.eng.usf.edu.(Accessed on 20.04.2015)
4. http://numericalmethods.eng.usf.edu. (Accessed on 19.03.2015)
5. Garrett, P., Absorption and Transmission of light and the Beer-Lambert Law, Lecture 21, 2006, www.physics.uoguelph.ca/~pgarrett/Teaching.html. (Accessed on 26.04.2015)
6. Mudakavi, J. R., Modern Instrumental Methods of Analysis, Lecture – 07, Ultraviolet and Visible Spectrophotometry – 3 Theoretical Aspects, http://nptel.ac.in/courses/103108100/7 (Accessed on 26.04.2015).
7. www.chemwiki.ucdavis.edu. (Accessed on 19.03.2015)

Tags: Buy essay USA, Custom Dissertation Writing Services for PhD Students, UK - Cheap Essay Writing Service, Write My Essay Fast - Plagiarism-Free AI Writing Tool